Post · bonfire.mavnn.eu

Post

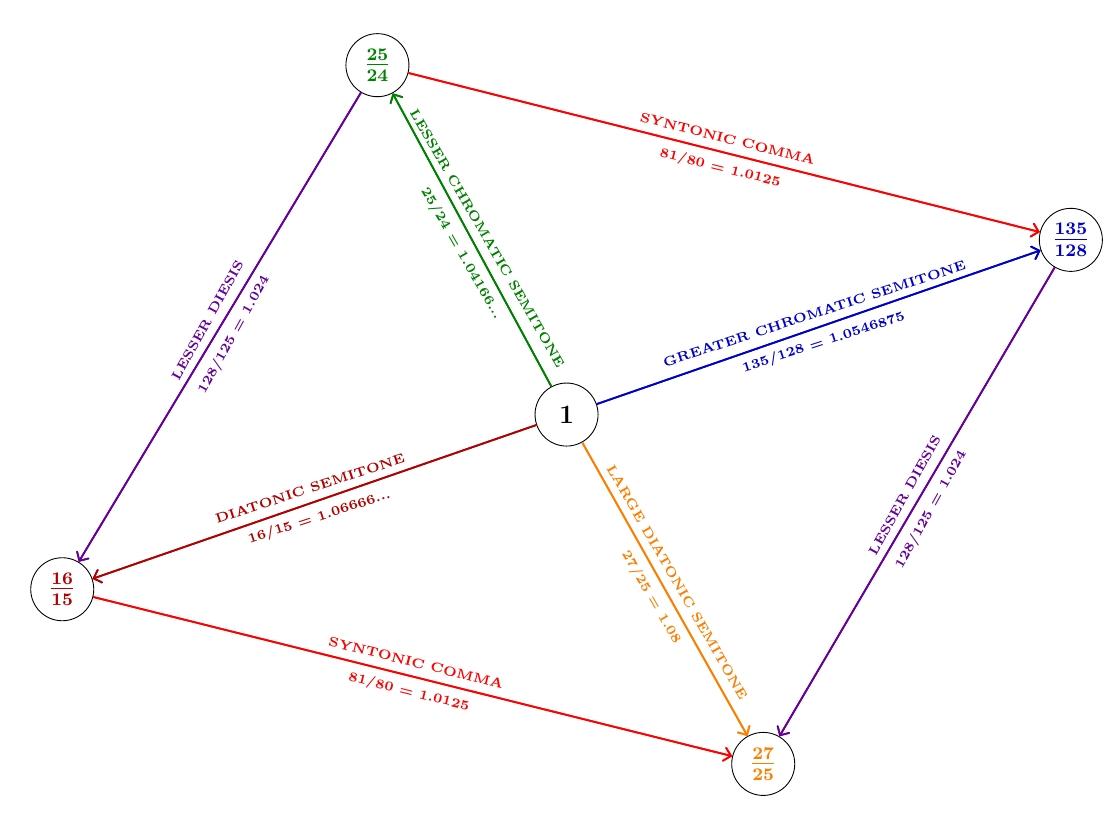
There are fascinating connections between the Riemann zeta function and music theory. I'll probably write a paper about this, but I can't resist talking about a little piece of the story now, as I'm still figuring it out.

Any commutative ring has a zeta function! The Riemann zeta function is the zeta function of ℤ, but the zeta function of ℤ/3 × ℤ/5 is simpler: it's just

1/(1 - 3⁻ˢ)(1 - 5⁻ˢ)

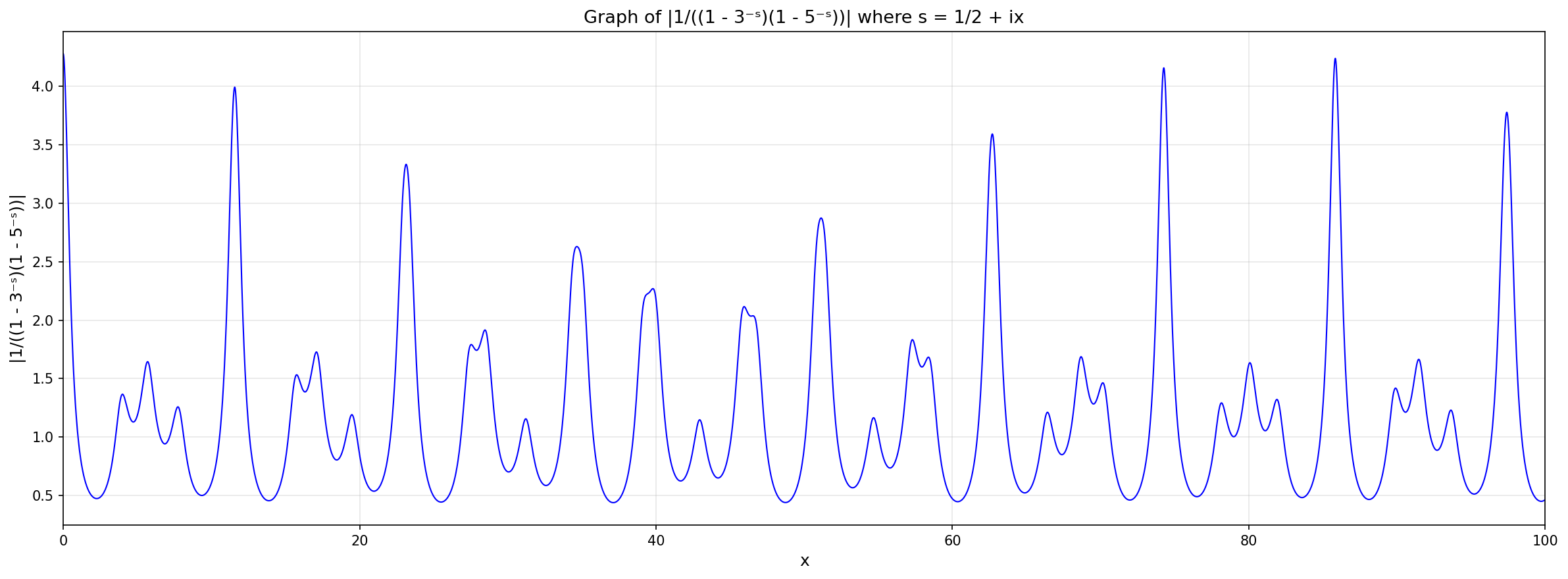
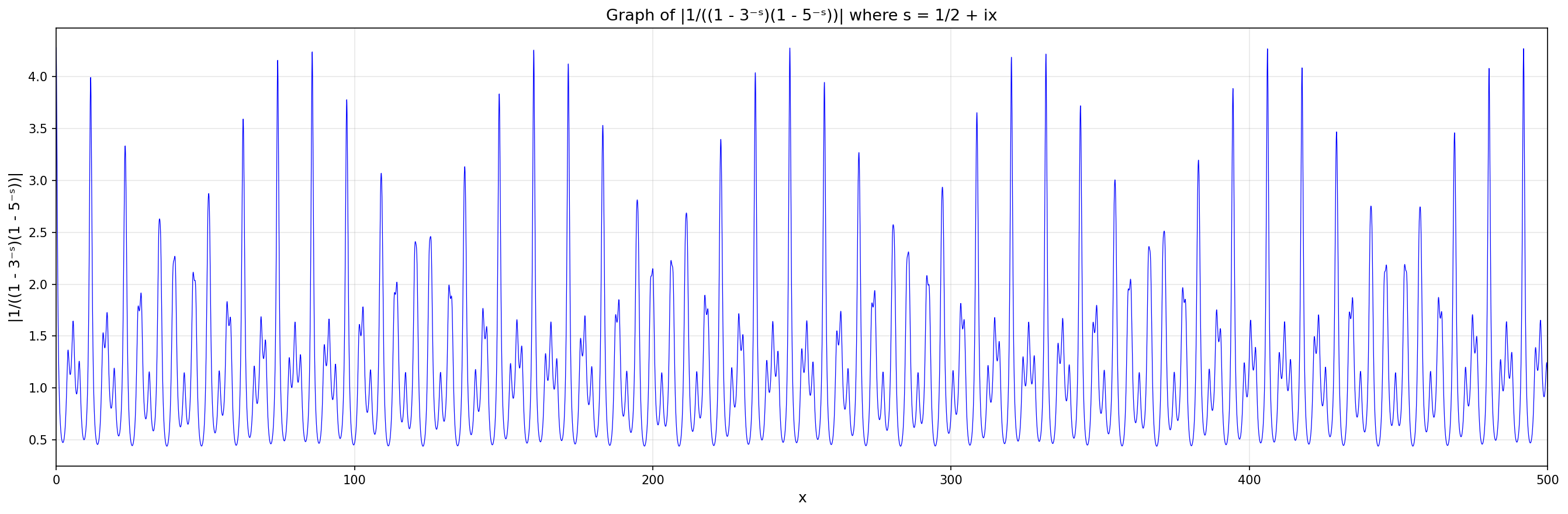
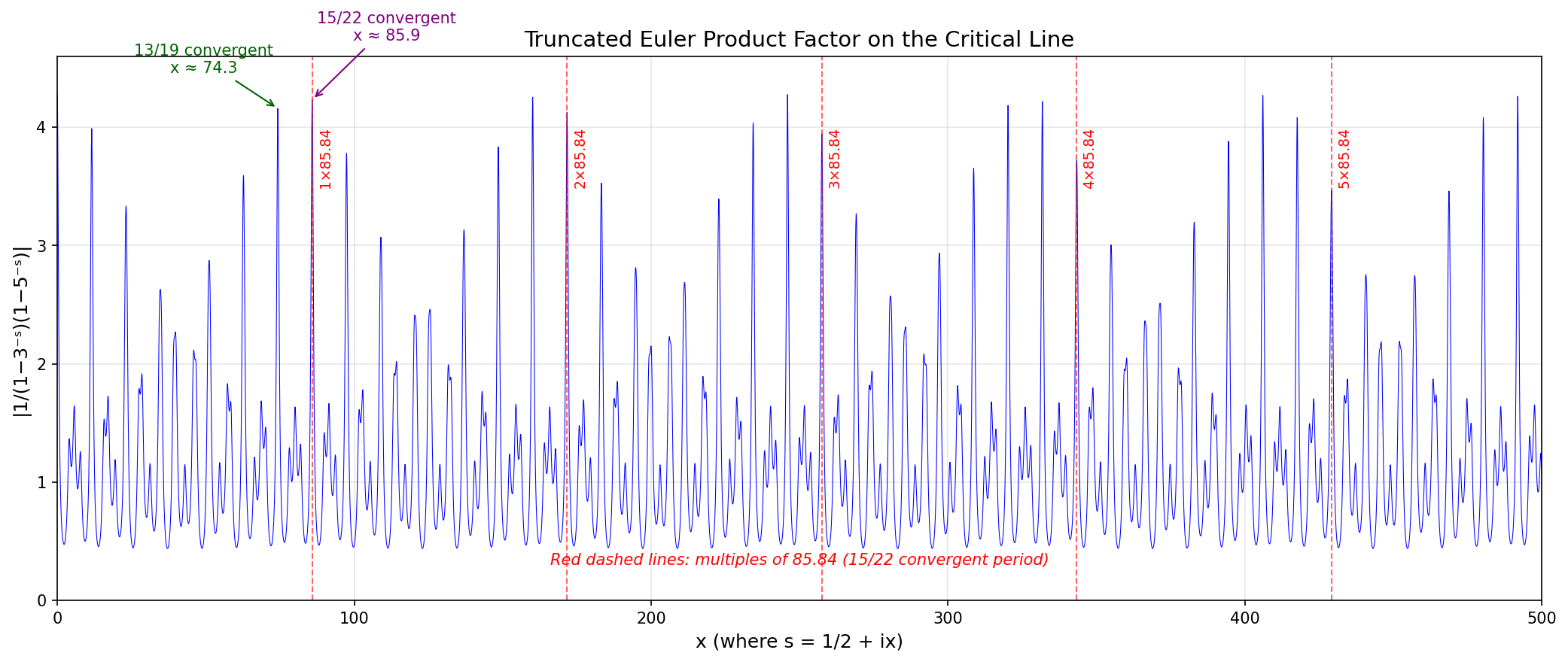
Let's graph this along the 'critical line' where the famous zeros of the Riemann zeta function live. So, let's take

s = ½ + ix

and plot

|1/(1 - 3⁻ˢ)(1 - 5⁻ˢ)|

as a function of x from x = 0 to x = 100. We get this picture here:

(1/n)

Graph of |1/(1 - 3⁻ˢ)(1 - 5⁻ˢ)| as a function of x from x = 0 to x = 100. It's a wiggly blue curve going between about 0.1 and 1, showing vibrations of various different frequencies: fast wiggles and slower 'beats'.

Andy Wootton

@[email protected] replied · 4 hours ago

@johncarlosbaez I was learning a little about 'Music Theory' when I discovered there is no good definition of what 'music' is. Having theories about something we can only describe by examples reminds me of computation.

It seems to me that some music comes from physics: selected highlights of the harmonic series gives us the pentatonic scale but the 12-note chromatic scale and the heptatonic scales are human inventions to try to make sense of what our ears tell us. That's more like religion.

Refurio Anachro

@[email protected] replied · 14 hours ago

Here's a complex plot up to 20i. White is the real axis and black purely imaginary. You can see a unit circle at the bottom.
@johncarlosbaez

John Carlos Baez

@[email protected] replied · 12 hours ago

@RefurioAnachro - Nice! Thanks! So far I'm entranced by its values on the critical line, and haven't dared venture off that line - since I don't know how it would help me.

julesh

@[email protected] replied · 16 hours ago

@johncarlosbaez I wonder what this looks like for rings that have very little to do with numbers, like boolean rings or rings of functions

John Carlos Baez

@[email protected] replied · 16 hours ago

@julesh - if the rings are "too infinite", like the ring of continuous real-valued functions on the real interval, the sum in the definition of the Hasse-Weil zeta function doesn't converge and we should probably leave it alone.

For finite boolean rings it's not so bad! For the 2-element ring with 'and' as times and 'exor' as plus, the zeta function is

1/(1 - 2ˢ).

(Whoops - just noticed a pile of minus sign typos I need to fix. Thanks!)

julesh

@[email protected] replied · 16 hours ago

@johncarlosbaez I wonder if there's some model theoretic universality result that all finite (or not too big) commutative rings embed into one specific commutative ring that involves numbers, like the ring of rationals or something like that?

John Carlos Baez

@[email protected] replied · 15 hours ago

@julesh - umm, no, because no commtuative ring where 1+1 = 0 embeds in any commutative ring without that property, and none without that property embeds in one that does have that property. This is why commutative algebraists (dually known as algebraic geometers) divide the world into different 'characteristics'. A ring of characteristic n has 1 + 1 + ... + 1 = 0 where you sum n ones. They especially like fields, and for fields each field either has characteristic p for some prime p or 'characteristic zero', meaning no sum of 1's can equal zero.

I am studying ℤ/3 × ℤ/5, which is a product of a field of characteristic 3 and one of characteristic 5. For many purposes these should be studied separately, but I enjoy seeing these 'beats' which appear when you combine different primes.

Alexander Knochel

@[email protected] replied · 17 hours ago

@johncarlosbaez Are the ring elements simply what I take the sum over in the \sum n^-x definition of the zeta function?

John Carlos Baez

@[email protected] replied · 16 hours ago

@Quantensalat - No, that's not how it works - the actual definition is here:

https://en.wikipedia.org/wiki/Hasse%E2%80%93Weil_zeta_function#Definition

But for rings that are products of fields with a prime number of elements, like

ℤ/3 × ℤ/11

ℤ/2 × ℤ/2 × ℤ/19 × ℤ/23

the zeta function takes a simple form, namely

1/(1 - 3⁻ˢ)(1 - 11⁻ˢ)

1/(1 - 2⁻ˢ)(1 - 2⁻ˢ)(1 - 19⁻ˢ)(1 - 23⁻ˢ)

etc.

John Carlos Baez

@[email protected] replied · 17 hours ago

To get a better picture of the *slow* oscillations in

|1/(1 - 3⁻ˢ)(1 - 5⁻ˢ)|

where s = ½ + ix, let's plot it from x = 0 to x = 300.

You can see a quasi-periodic oscillations with multiple timescales - rapid wiggles modulated by a slower beating pattern. I want to understand what's going on here.

(2/n)

Graph of |1/(1 - 3⁻ˢ)(1 - 5⁻ˢ)| as a function of x from x = 0 to x = 500. It's a wiggly blue curve going between about 0.1 and 1, showing vibrations of various different frequencies: fast wiggles and slower 'beats'. The larger range of x makes it easier to see beats of period roughly - very roughly! - 100.

Strider Uwe 🇺🇦🇨🇦🇲🇽

@[email protected] replied · 5 hours ago

@johncarlosbaez Are you sure that you are plotting with high enough resolution that you know for a fact where and how tall all those peaks are? Ie, the picture doesn’t change visibly if you double or triple the resolution? I ask because these variations remind me of graphs I’ve made in very different context, and fairly smooth curves start to get these beats as the sampling gets coarser. In my case these were more sampling artifacts, not sure here but it’s worth checking?

John Carlos Baez

@[email protected] replied · 4 hours ago

@UweHalfHand - If I didn't have good theoretical/intuitive reasons to expect these beats I would be more suspicious of what I'm seeing. I am suspicious of the height and especially the *width* of the spikes in the Fourier transform of the absolute value of this zeta function - they could easily be delta functions. But I'm not surprised to be getting spikes at frequencies of the form ln(3ʲ5ᵏ)/2π), because if we omit the absolute value, the Fourier transform of the zeta function itself is a weighted sum of delta functions at all possible numbers of the form ln(3ʲ5ᵏ)/2π).

Still, your point is a good one: if I ever want to publish anything about this I should check it more carefully.

John Carlos Baez

@[email protected] replied · 17 hours ago

In the graph here, the tall sharp spikes are spaced by a distance of about

11.58

On the other hand, the crests of the long waves are spaced by a distance of about

85.84

I'll try to figure out why. Bu you can try too, if you enjoy this kind of puzzle.

We can take the reciprocal of the zeta function and notice that

(1 - 3⁻ˢ)(1 - 5⁻ˢ) = 1 - √3 e^(ix ln 3) - √5 e^(ix ln 5) + √15 e^(ix ln 15)

So for *this* function we expect oscillations with periods

2π/ln(3) ≈ 5.719
2π/ln(5) ≈ 3.904
2π/ln(15) = 2π/(ln(3) + ln(5)) ≈ 2.320

but this does not instantly explain the longer periods that stand out so dramatically in the graph here!

(3/n)

Graph of |1/(1 - 3⁻ˢ)(1 - 5⁻ˢ)| as a function of x from x = 0 to x = 500. It's a wiggly blue curve going between about 0.44 and 4.28, showing vibrations of various different frequencies: fast wiggles and slower 'beats'. The larger range of x makes it easier to see beats of period roughly 62.69.

John Carlos Baez

@[email protected] replied · 15 hours ago

The slow 'beats' in the absolute value of the zeta function

1/(1 - 3⁻ˢ)(1 - 5⁻ˢ)

arise because it's the product of two functions: 1/(1 - 3⁻ˢ) which has period

2π/ln(3) ≈ 5.719

as a function of x (remember s = ½ + ix), and 1/(1 - 5⁻ˢ) which has period

2π/ln(5) ≈ 3.904

as a function of x.

These functions both become big at the same point x when there are integers m,n with

x ≈ m 2π/ln(3) ≈ n 2π/ln(5)

This requires

m/n ≈ ln(3)/ln(5)

So finding the tallest peaks in the absolute value of the zeta function amounts to looking for good rational approximations of this number:

ln(3)/ln(5) ≈ 0.682606194

Here are the first few:

2/3 ≈ 0.6667
13/19 ≈ 0.6842
15/22 ≈ 0.6818

The first says we expect tall peaks spaced apart by roughly

2 × [2π/ln(3)] ≈ 3 × [2π/ln(5)]

These numbers are close but not equal! Look at them:

4π/ln(3) ≈ 11.44
6π/ln(5) ≈ 11.71

This explains why I empirically found that the tall sharp spikes in the graph below are separated by a distance of about 11.58. I don't know a formula yet that gives 11.58, but I see why it's between those two numbers!

(4/n)

Sylvain

@[email protected] replied · 14 hours ago

@johncarlosbaez

It may not have any relevance whatsoever and could be my mind seeing things that don't exist. I am no mathematician or muscian, but in the graph you shared, all I can see is these three overlapping waves.

Screen capture of the graph shared by Mr Baez, but with three (badly) hand drawn lines over it, outlining three seemingly identical, overlapping waves, each starting a third of the wave length farther right on the x axis.

(This description is probably the worst in the history of mathematics... sorry) — Screen capture of the graph shared by Mr Baez, but with three (badly) hand drawn lines over it, outlining three seemingly identical, overlapping waves, each starting a third of the wave length farther right on the x axis. (This description is probably the worst in the history of mathematics... sorry)

John Carlos Baez

@[email protected] replied · 13 hours ago

@axnxcamr - I saw the waves, and I'm working toward understanding them, but I hadn't noticed that there were 3 interlocking waves. So thanks for pointing that out: that's important.

I had said that the distance between successive wave crests is about 62.69, which actually looks wrong to me now. Anyway, the right thing to look at might be the distance between successive wave crests of the same color. Or maybe not!

So far I've only figured out why the distance between very tall sharp spikes is close to 11.58. That's what I did in post 4. In post 5, I showed that this happens because 3³ is close to 5², i.e. 27 is close to 25.

Other features should arise from other aspects of the interplay between the numbers 3 and 5.

John Carlos Baez

@[email protected] replied · 14 hours ago

But what does all this have to do with music?

The fact that 2/3 is a good rational approximation to ln(3)/ln(5) says that

3 ln(3) ≈ 2 ln(5)

or exponentiating both sides,

3³ ≈ 5²

i.e.

27 ≈ 25.

The ratio 27/25 is so important in music that it has a name! It's called the 'large diatonic semitone'. It's one of four semitones that naturally show up in just intonation.

Just intonation is ruled by the primes 2, 3, and 5, but today I'm just looking at the primes 3 and 5. That's why I'm looking at the zeta function of the commutative ring ℤ/3 × ℤ/5, and that's why the number 27/25 showed up! It's the simplest fraction quite close to 1 that you can build from powers of 3 and 5.

(5/n)

A parallelogram whose corners are 4 semitones used in just intonation: the lesser chromatic semitone 25/24, the greater chromatic semitone 135/128, the diatonic semitone 16/15 and the large diatonic semitone 27/25. At the center is the number 1. The edges are also labeled by fractions important in music theory: the syntonic comma 81/80 and lesser diesis 128/125.

John Carlos Baez

@[email protected] replied · 13 hours ago

Now I think I see why the distance between crests of the big long waves in this graph is about 85.84!

We saw

ln(3)/ln(5) ≈ 2/3

gives spikes in this graph spaced at a distance of about

2 × [2π/ln(3)] ≈ 3 × [2π/ln(5)]

These numbers are 11.44 and 11.71, respectively. The actual spike spacing is about halfway between these two.

Similarly, the better approximation

ln(3)/ln(5) ≈ 13/19

should give peaks spaced at a distance of about

13 × [2π/ln(3)] ≈ 19 × [2π/ln(5)]

These numbers are 74.35 and 74.17, respectively.

Alas, that's not explaining our number 85.84. 😢

But there's an even better approximation

ln(3)/ln(5) ≈ 15/22

which should give peaks spaced at a distance of about

15 × [2π/ln(3)] ≈ 22 × [2π/ln(5)]

and these numbers are 85.79 and 85.89. The number 85.84 is about halfway between these two!!! 🎉

Of course this is still a bit mysterious. Why does 15/22 do something for us, but apparently not 13/19?

Actually I believe 13/19 *does* do something for us. I'm just not sure what.

I also haven't studied what even better rational approximations to ln(3)/ln(5) do for us. But I imagine they create subtler waves in the zeta function, with even longer periods.

(6/n)

John Carlos Baez

@[email protected] replied · 12 hours ago

Aha! 💡

Now I see what the number 13/19 being close to ln(3)/ln(5) does for us.

I said it predicts peaks in our zeta function spaced at a distance of roughly 74.3. And indeed, there are big peaks at x = 0 and x ≈ 74.3!

There's a bigger peak at x ≈ 85.84, since the number 15/22 is even closer to ln(3)/ln(5).

But I was wrong in suggesting that the period of the really big waves is 85.84! In fact the multiples of 85.84 drift away from crests of those waves.

But you'll notice they do lie on sharp spikes.

And this is only possible because

85.84 - 74.3 = 11.54

which is very close to the distance between the sharp spikes!!! Remember, I computed that distance approximately in part 4, that using the fact that 2/3 is another rational approximation to ln(3)/ln(5).

But where does the above equation come from? Is it a coincidence?

No, earlier in this thread we computed numbers 85.84, 74.3 and 11.54 approximately in two different ways. If we use one of these ways, 85.84 - 74.3 = 11.54 is telling us

15 × [2π/ln(3)] - 13 × [2π/ln(3)] = 2 × [2π/ln(3)]

If we use the other, it's telling us

22 × [2π/ln(5)] - 19 × [2π/ln(5)] = 3 × [2π/ln(5)]

Both of these are of course true!

So, something very nice is going on here. But I'm still confused about what.

(7/n)