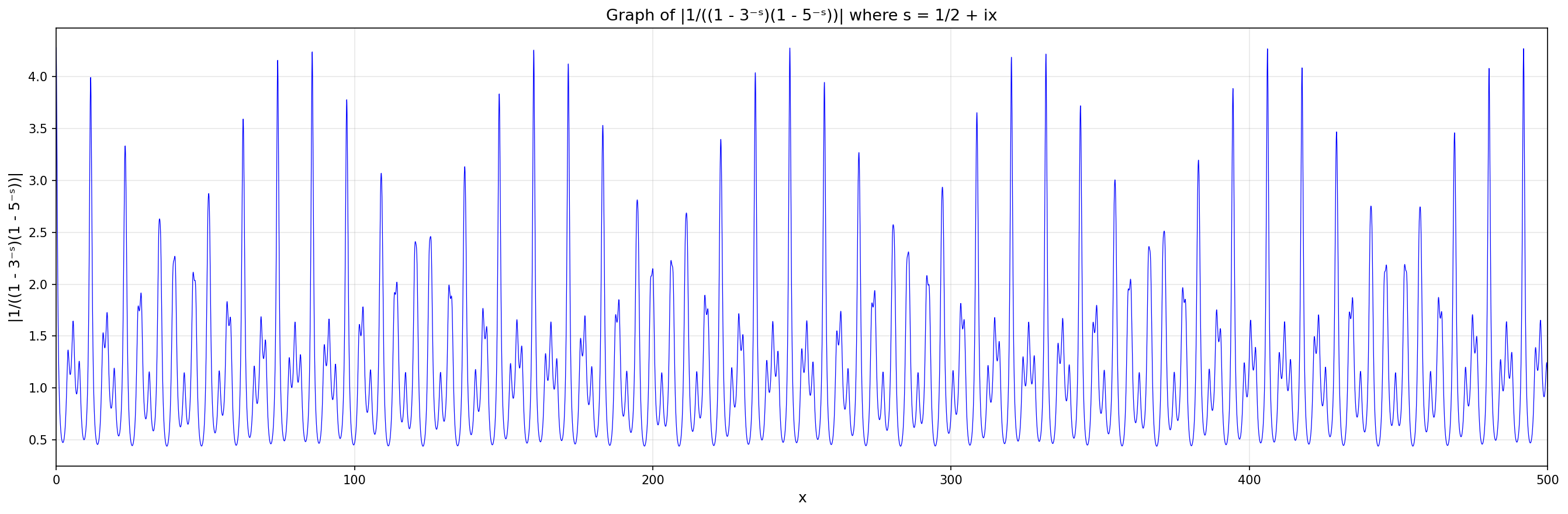
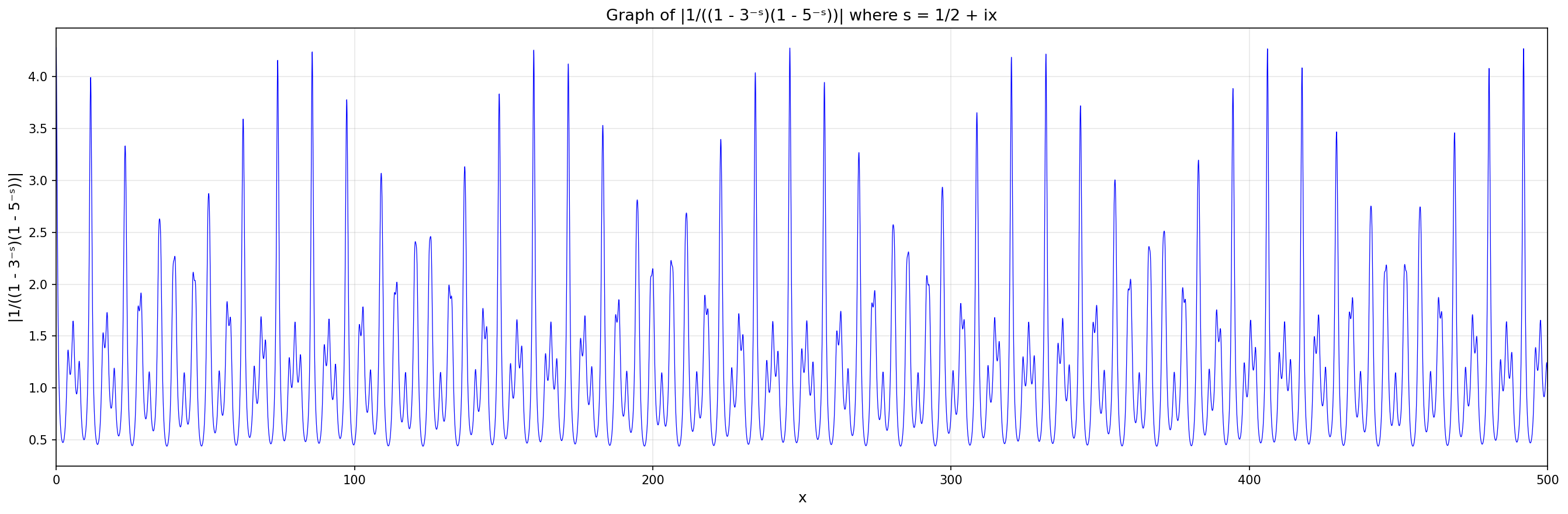
So far I've been trying to understand the complicated waves in the function
|1/(1−3^{-(1/2) - ix})(1−5^{-(1/2) - ix})|
@SvenGeier suggested that it would help to compute the Fourier transform this function.
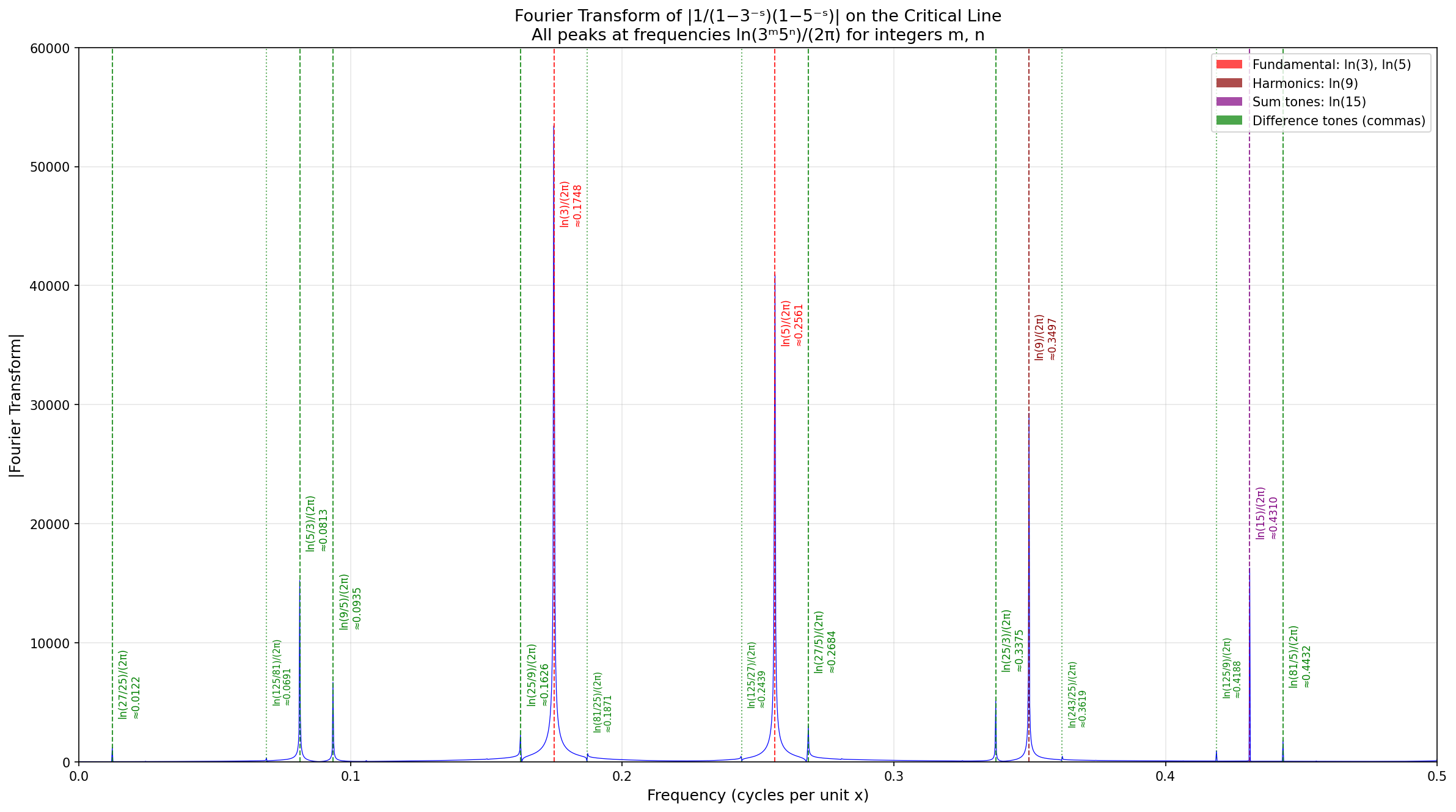
This was indeed very revealing. Check out the graph below!
There are the expected big peaks at
ln(3)/2π
ln(5)/2π
ln(15)/2π
which we expect from part 3. But there are many more - and many with musical significance! Let me list them - but instead of writing each frequencies ω, which are always of the form ln(a)/2π for rational numbers a, I'll just write the numbers a. Some have fairly simple musical names:
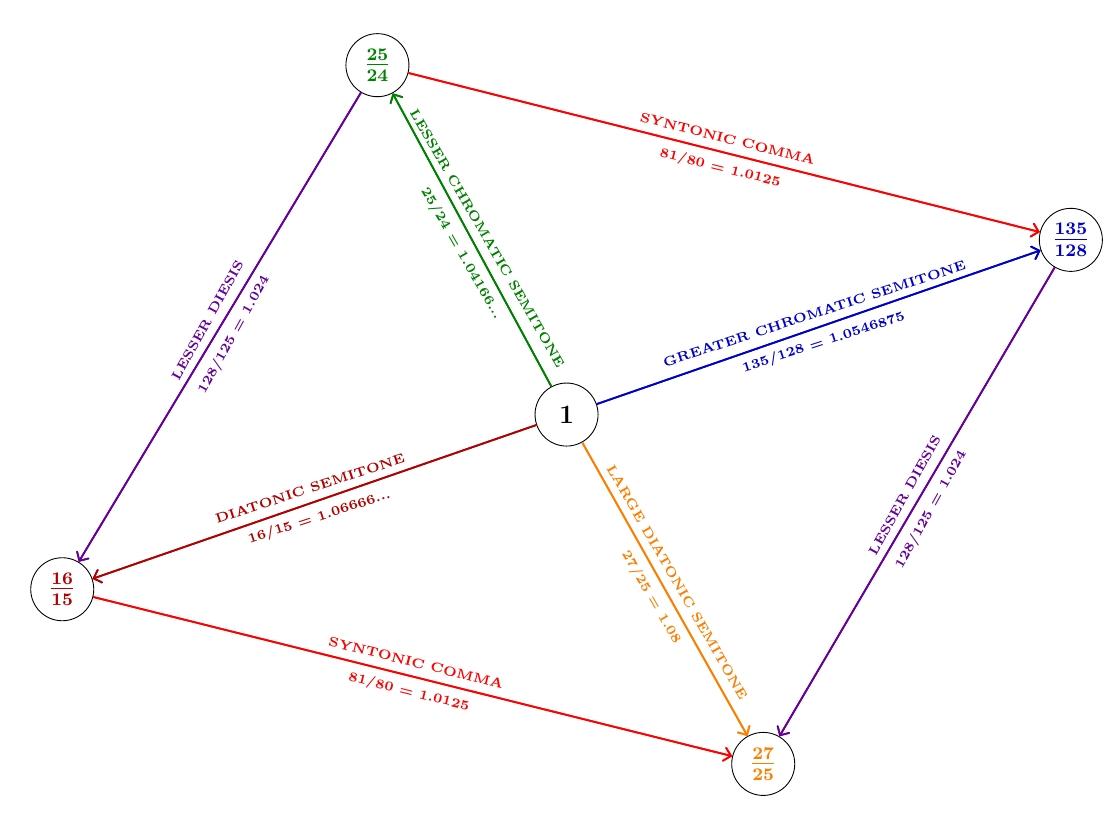
0.0122 27/25 large diatonic semitone
0.0813 5/3 major sixth
0.0935 9/5 minor seventh
0.1626 25/9 two major thirds
0.1748 3 perfect twelfth
0.2561 5 major third + two octaves
0.2684 27/5
0.3375 25/3
0.3497 9 two twelfths
0.4188 125/9
0.4310 15
0.4432 81/5
The musical names are probably less informative than the patterns here.
Some of these peaks are barely visible. There are probably more too small to see - infinitely many of them!
(9/n)